Find The General Solution Of The Given System Of Equations
Solved Find The General Solution To The Given System Of Chegg Com
Find the general solution of the given system of equations. Finding a general equation for a given sequence requires a lot of thinking and practice but learning the specific rule guides you in discovering the general equation. We also need these two numers to equal -1 when we add them because -1 is the coefficient of the x term. Most of the cases you can find the exact solutions for the given math equations.
Recall that a linear equation can take the form latexAxByC0latex. The power series method can be applied to certain nonlinear differential equations though with less flexibility. We will develop methods for exact solutions in later sections.
The general solution is. Math equations allow you to solve an equation or a system of equations. Solve Equations with Fractions or Decimals.
When we solve radical equations by squaring both sides we may get an algebraic solution that would make negative. A system of nonlinear equations is a system of two or more equations in two or more variables containing at least one equation that is not linear. Use a General Strategy to Solve Linear Equations.
B No solution C Infinitely many solutions D None of these. Citation needed An overdetermined system is almost always inconsistent it has no solution when constructed with random coefficientsHowever an overdetermined system will have solutions in some cases for example if some equation occurs several times in the system or if some. So for these given initial conditions we can find a combination of the constants A and φ so this is the general solution.
The force of gravity is given by mgmg. Linear equations considered together in this fashion are said to form a system of equations. How many boundary conditions.
Note that each frequency is used twice because our solution was for the square of the frequency. Y -3x 7.
Solved Find The General Solution To The Given System Of Chegg Com
Find The General Solution Of The Given System Of Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Solved Find The General Solution To The Given System Of Chegg Com
Solved 6 Find The General Solution Of The Given System Of Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Oneclass Find The General Solution Of The Given System Of Equations Find The General Solution Of T
Math 4 B Systems Of Differential Equations Nonhomogeneous
Solved Find The General Solution Of The Given System Of Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Answered Find The General Solution Of The Given Bartleby
Solved Find The General Solution Of The Given System Of Chegg Com
Answered Find The General Solution Of The Given Bartleby
Solved Find The General Solution Of The Given System Of Chegg Com
Solved Chapter 7 Section 7 8 Question 01c Find The General Solution Of The Given System Of Equations Ww A 7 20 66t 62 Ret L E6 Course Hero
Solved In Each Of Problems 1 Through 12 Find The General Solution Of The Given System Of Equations 13 X X 2 X C Cos 3 X X
Answered Find The General Solution Of The Given Bartleby
Solved Find The General Solution To The Given System Of Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Solved Use The Elimination Method To Find General Solution For The Given Linear System Where Differentiation Is With Respect To T 2x Y 9x Ty E X Y 4x
Answered Find The General Solution Of The Given Bartleby
Solved In Each Of Problem 9 Through 14 Find The General Chegg Com
Solved Find The General Solution Of The Given System Of Chegg Com
Solved 10 Use The Elimination Method T0 Find General Solution For The Given Linear System Where Differentiation Is With Respect To T Dx Dt 5x 4y A 4x Sy Eliminate X
Find The General Solution Of The Given System Of Equat Itprospt
Solved Chapter 7 Section 7 9 Question 04 Find The General Chegg Com
Solving Systems Of Equations Using Algebra Calculator Mathpapa
Chapter 3 Section 3 3 Question 02 Consider The Given System Of Equation 2 4 X 6 8 A Find The General Solution Of Homeworklib
Answered Find The General Solution Of The Given Bartleby
Differential Equations Solved Examples Find The General Solution Of The Given System Of Differential Equations Dx Dt 10x 8y Dy Dt 11x 8 2y
Solved Chapter 7 Section 7 6 Go Tutorial Problem 04 Find The General Solution To The Given System Of Equations 2 Cos 3 2 Sin 3 Cos 3 3 Sin Course Hero
1 Points Boycediffeq10 7 9 001 Find The General So Itprospt
Solved In Each Of Problems 1 Through 12 Find The General Chegg Com
Differential Equations Solved Examples Find The General Solution Of The Given System Using Method Of Eigenvalues Dx Dt 7x 4y Dy Dt X 2z Dz Dt 2y 7z
Solved 3 20 20 10 50 Points Find The General Solution Of The Given System Of Equations T 12 Find The Eigenvalues Of The Corresponding Matrix Find The Eigenvectors Of The Corresponding Matrix Write Down
Example Finding The General Solution To Linear Equations By First Finding A Particular Solution Youtube
8 In Each Of Problems 7 Through 9 Find The General Solution Of The Given System Homeworklib
Solved Find The General Solution Of The Given System Of Chegg Com
11 Points Zilldiffeq9 8 2 037 Find The General Solu Itprospt
Use The Elimination Method To Find A General Solution For The Given Linear System Where Differentiation Homeworklib
Systems Of Equations Solver Wolfram Alpha
Math 4b Systems Of Differential Equations Matrix Solutions Prepared By Vince Zaccone For Campus Learning Assistance Services At Ucsb Ppt Download
Solving A System 3 Equations General Solution Youtube
Oneclass Plzzzzzzzzz Help Me Out Find The General Solution For Each Of The Given System Of Equation
Solved Find The General Solution Of The Given System X Chegg Com
16 Please Help Me Solve The Following Differential Equations Problem Consider The Following A Computer Algebra System Is Recommended X 1か 1 4 A Find The General Solution To The Given Sys Homeworklib
Solving Systems Of Linear Equations Lesson Article Khan Academy
So for these given initial conditions we can find a combination of the constants A and φ so this is the general solution.
Types of Linear Systems. Use a General Strategy to Solve Linear Equations. A very large class of nonlinear equations can be solved analytically by using the ParkerSochacki methodSince the ParkerSochacki method involves an expansion of the original system of ordinary differential equations through auxiliary equations it is not. Here a 1 a 2 b 1 b 2 c 1 c 2. So this system of equations has no solution. How many boundary conditions. In mathematics a system of equations is considered overdetermined if there are more equations than unknowns. We also need these two numers to equal -1 when we add them because -1 is the coefficient of the x term. There are three types of systems of linear equations in two variables and three types of solutions.
We will develop methods for exact solutions in later sections. This may be done by collecting a small constant volume of sample and compositing it for a day or a week or it may be done by collecting a given volume at random times or on a regular schedule. Similar considerations apply to sets of linear equations with more than one unknown. This system must be sampled at many different times to collect a representative sample. So this system of equations has no solution. This would be more work and if 7 1 is represented to a finite number of digits less accurate. Consider the forces acting on the mass.
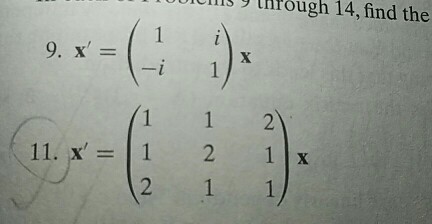
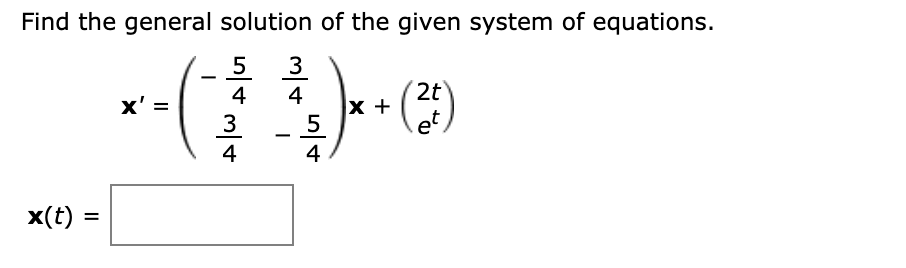
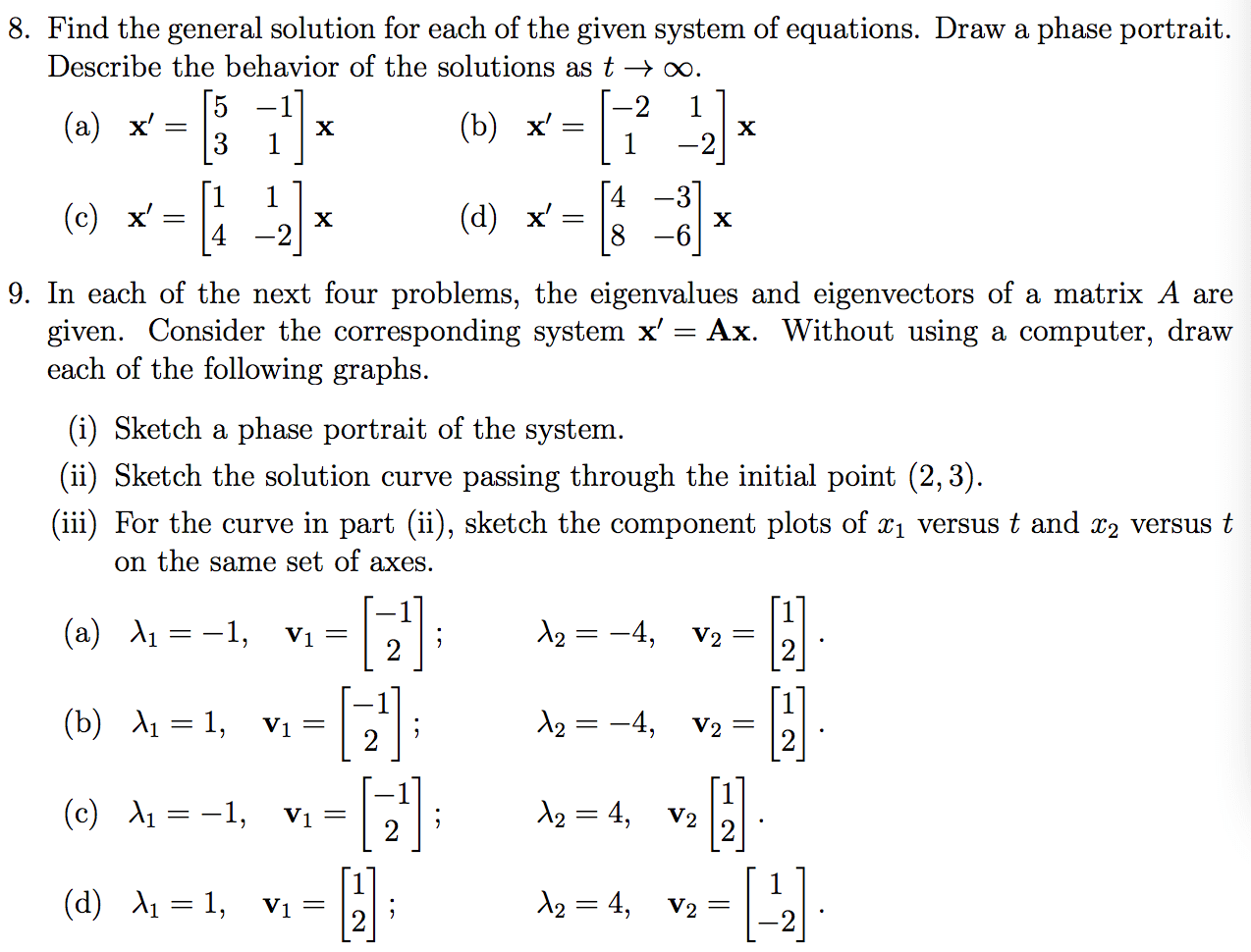
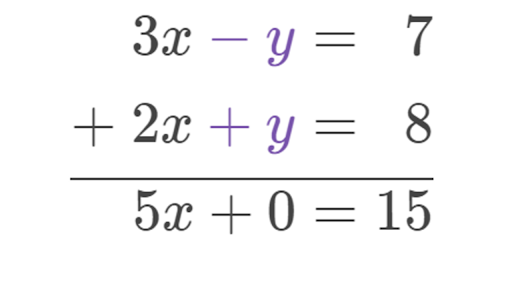
Post a Comment for "Find The General Solution Of The Given System Of Equations"